前言

本文介绍几种经典、常考的内排序算法。

本文试图建立一个比较标准的快速排序、归并排序、堆排序算法代码。

选择排序

了解。

算法思想

每一轮选取未排定的部分中最小的部分交换到未排定部分的最开头，经过若干个步骤，就能排定整个数组。即：先选出最小的，再选出第 2 小的，以此类推。

实现

略

插入排序

了解

算法思想

每次将一个数字插入一个有序的数组里，成为一个长度更长的有序数组，有限次操作以后，数组整体有序。

实现

略

冒泡排序

了解

算法思想

外层循环每一次经过两两比较，把每一轮未排定部分最大的元素放到了数组的末尾；
「冒泡排序」有个特点：在遍历的过程中，提前检测到数组是有序的，从而结束排序，而不像「选择排序」那样，即使输入数据是有序的，「选择排序」依然需要「傻乎乎」地走完所有的流程。

实现

略

希尔排序

了解

算法思想

插入排序的优化。在插入排序里，如果靠后的数字较小，它来到前面就得交换多次。「希尔排序」改进了这种做法。带间隔地使用插入排序，直到最后「间隔」为 11 的时候，就是标准的「插入排序」，此时数组里的元素已经「几乎有序」了。

实现

略

快速排序

重要

算法思想

快速排序每一次都排定一个元素（这个元素呆在了它最终应该呆的位置），然后递归地去排它左边的部分和右边的部分，依次进行下去，直到数组有序。

实现（递归）

//https://mp.weixin.qq.com/s/8ZTMhvHJK_He48PpSt_AmQ
class Quick {

    public static void sort(int[] nums) {
        // 为了避免出现耗时的极端情况，先随机打乱
        shuffle(nums);
        // 排序整个数组（原地修改）
        sort(nums, 0, nums.length - 1);
    }

    private static void sort(int[] nums, int lo, int hi) {
        if (lo >= hi) {
            return;
        }
        // 对 nums[lo..hi] 进行切分
        // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
        int p = partition(nums, lo, hi);

        sort(nums, lo, p - 1);
        sort(nums, p + 1, hi);
    }

    // 对 nums[lo..hi] 进行切分
    private static int partition(int[] nums, int lo, int hi) {
        int pivot = nums[lo];
        // 关于区间的边界控制需格外小心，稍有不慎就会出错
        // 我这里把 i, j 定义为开区间，同时定义：
        // [lo, i) <= pivot；(j, hi] > pivot
        // 之后都要正确维护这个边界区间的定义
        int i = lo + 1, j = hi;
        // 当 i > j 时结束循环，以保证区间 [lo, hi] 都被覆盖
        while (i <= j) {
            while (i < hi && nums[i] <= pivot) {
                i++;
                // 此 while 结束时恰好 nums[i] > pivot
            }
            while (j > lo && nums[j] > pivot) {
                j--;
                // 此 while 结束时恰好 nums[j] <= pivot
            }
            // 此时 [lo, i) <= pivot && (j, hi] > pivot

            if (i >= j) {
                break;
            }
            swap(nums, i, j);
        }
        // 将 pivot 放到合适的位置，即 pivot 左边元素较小，右边元素较大
        swap(nums, lo, j);
        return j;
    }

    // 洗牌算法，将输入的数组随机打乱
    private static void shuffle(int[] nums) {
        Random rand = new Random();
        int n = nums.length;
        for (int i = 0 ; i < n; i++) {
            // 生成 [i, n - 1] 的随机数
            int r = i + rand.nextInt(n - i);
            swap(nums, i, r);
        }
    }

    // 原地交换数组中的两个元素
    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

实现（非递归）

暂略

归并排序

重要

算法思想

借助额外空间，合并两个有序数组，得到更长的有序数组。

实现

class Merge {

    // 用于辅助合并有序数组
    private static int[] temp;

    public static void sort(int[] nums) {
        // 先给辅助数组开辟内存空间
        temp = new int[nums.length];
        // 排序整个数组（原地修改）
        sort(nums, 0, nums.length - 1);
    }

    // 定义：将子数组 nums[lo..hi] 进行排序
    private static void sort(int[] nums, int lo, int hi) {
        if (lo == hi) {
            // 单个元素不用排序
            return;
        }
        // 这样写是为了防止溢出，效果等同于 (hi + lo) / 2
        int mid = lo + (hi - lo) / 2;
        // 先对左半部分数组 nums[lo..mid] 排序
        sort(nums, lo, mid);
        // 再对右半部分数组 nums[mid+1..hi] 排序
        sort(nums, mid + 1, hi);
        // 将两部分有序数组合并成一个有序数组
        merge(nums, lo, mid, hi);
    }

    // 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
    private static void merge(int[] nums, int lo, int mid, int hi) {
        // 先把 nums[lo..hi] 复制到辅助数组中
        // 以便合并后的结果能够直接存入 nums
        for (int i = lo; i <= hi; i++) {
            temp[i] = nums[i];
        }

        // 数组双指针技巧，合并两个有序数组
        int i = lo, j = mid + 1;
        for (int p = lo; p <= hi; p++) {
            if (i == mid + 1) {
                // 左半边数组已全部被合并
                nums[p] = temp[j++];
            } else if (j == hi + 1) {
                // 右半边数组已全部被合并
                nums[p] = temp[i++];
            } else if (temp[i] > temp[j]) {
                nums[p] = temp[j++];
            } else {
                nums[p] = temp[i++];
            }
        }
    }
}

堆排序

重要

算法思想

将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列。

实现

public class Solution {

    public int[] sortArray(int[] nums) {
        int len = nums.length;
        // 将数组整理成堆
        heapify(nums);

        // 循环不变量：区间 [0, i] 堆有序
        for (int i = len - 1; i >= 1; ) {
            // 把堆顶元素（当前最大）交换到数组末尾
            swap(nums, 0, i);
            // 逐步减少堆有序的部分
            i--;
            // 下标 0 位置下沉操作，使得区间 [0, i] 堆有序
            siftDown(nums, 0, i);
        }
        return nums;
    }

    /**
     * 将数组整理成堆（堆有序）
     *
     * @param nums
     */
    private void heapify(int[] nums) {
        int len = nums.length;
        // 只需要从 i = (len - 1) / 2 这个位置开始逐层下移
        for (int i = (len - 1) / 2; i >= 0; i--) {
            siftDown(nums, i, len - 1);
        }
    }

    /**
     * @param nums
     * @param k    当前下沉元素的下标
     * @param end  [0, end] 是 nums 的有效部分
     */
    private void siftDown(int[] nums, int k, int end) {
        while (2 * k + 1 <= end) {
            int j = 2 * k + 1;
            if (j + 1 <= end && nums[j + 1] > nums[j]) {
                j++;
            }
            if (nums[j] > nums[k]) {
                swap(nums, j, k);
            } else {
                break;
            }
            k = j;
        }
    }

    private void swap(int[] nums, int index1, int index2) {
        int temp = nums[index1];
        nums[index1] = nums[index2];
        nums[index2] = temp;
    }
}

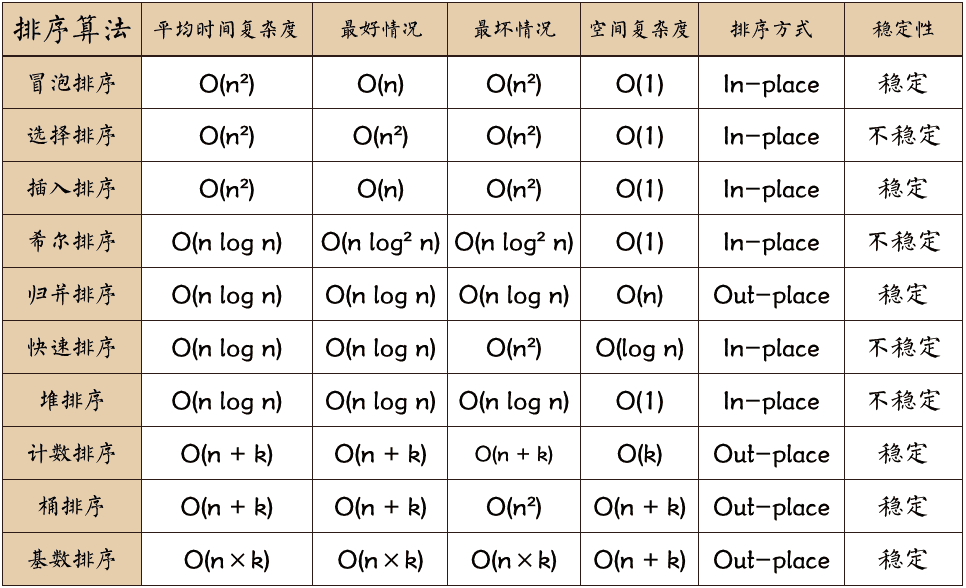
排序复杂度比较

参考资料

1. 复习基础排序算法
2. 菜鸟教程：十大排序算法
3. 《算法 第四版》
4. 快速排序的正确理解方式及运用
5. 归并排序的正确理解方式及运用